最近看瞭一系列bilinear pooling相關的文章,感覺有些文章寫得比較抽象。費瞭不少功夫總算理順瞭這些文章的關系,這裡簡單寫個筆記記錄一下~
- 簡介
bilinear pooling在2015年於《Bilinear CNN Models for Fine-grained Visual Recognition》被提出來用於fine-grained分類後,又引發瞭一波關註。bilinear pooling主要用於特征融合,對於從同一個樣本提取出來的特征 x 和特征 y ,通過bilinear pooling得到兩個特征融合後的向量,進而用來分類。
如果特征 x 和特征 y來自兩個特征提取器,則被稱為多模雙線性池化(MBP,Multimodal Bilinear Pooling);如果特征 x =特征 y,則被稱為同源雙線性池化(HBP,Homogeneous Bilinear Pooling)或者二階池化(Second-order Pooling)。此外,有些文章也把bilinear model稱為bilinear pooling(這麼做是有原因的,下文會分析)。
原始的Bilinear Pooling存在融合後的特征維數過高的問題,融合後的特征維數=特征 x 和特征 y的維數之積。原作者嘗試瞭PCA降維,但效果並不理想。基於降低bilinear pooling特征維數的思想,近年來的改進方案參見下表:
本文將包括以下內容:
- 對bilinear pooling進行詳細介紹,便於讀者理解原文;
- 建立bilinear pooling到bilinear model的聯系,便於讀者理解以MLB為核心的bilinear model相關文章。
- 快速介紹對bilinear pooling的各種改進形式。
- bilinear pooling詳解
這裡參考《Bilinear CNN Models for Fine-grained Visual Recognition》,CVPR 2015一文,給出bilinear pooling的詳細定義。
對於圖像 mathcal{I} 在位置 l 的兩個特征 f_A(l, mathcal{I}) in mathbb{R}^{T times M} 和 f_B(l, mathcal{I}) in mathbb{R}^{T times N} , 進行如下操作:
begin{align*} b(l, mathcal{I}, f_A, f_B) &= f_A^T(l, mathcal{I})f_B(l, mathcal{I}) &in mathbb{R}^{M times N}, \ xi(mathcal{I}) &= sum_l b(l, mathcal{I}, f_A, f_B) &in mathbb{R}^{M times N}, \ x &= text{vec}(xi(mathcal{I})) &in mathbb{R}^{MN times 1}, \ y &= text{sign}(x)sqrt{|x|} &in mathbb{R}^{MN times 1}, \ z &= y/||y||_2 &in mathbb{R}^{MN times 1}, \ end{align*}
直觀上理解,所謂bilinear pooling,就是先把在同一位置上的兩個特征雙線性融合(相乘)後,得到矩陣 b ,對所有位置的 b 進行sum pooling(也可以是max pooling,但一般采用sum pooling以方便進行矩陣運算)得到矩陣 xi ,最後把矩陣 xi 張成一個向量,記為bilinear vector x 。對x進行矩歸一化操作和L2歸一化操作後,就得到融合後的特征 z 。之後,就可以把特征 z用於fine-grained分類瞭,如下圖所示:
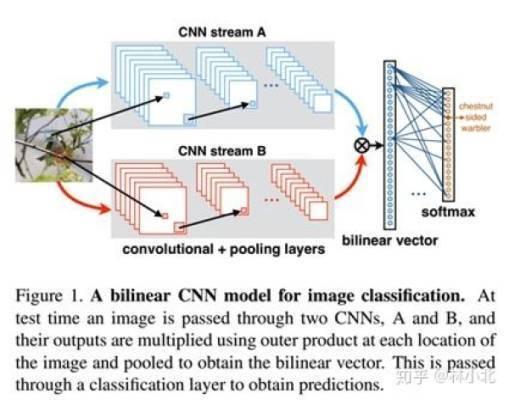
對於我們熟悉的圖像特征, T=1 ,而 M 和 N 分為別特征的通道數,把兩個特征分別寫成向量 mathbf{a}_l=f_A^T(l, mathcal{I}) in mathbb{R}^{M times 1} 和 mathbf{b}_l=f_B^T(l, mathcal{I}) in mathbb{R}^{N times 1} ,有
xi(mathcal{I}) = sum_l mathbf{a}_lmathbf{b}_l^T in mathbb{R}^{M times N}.
記 mathbf{A}=[mathbf{a}_1, cdots, mathbf{a}_L] in mathbb{R}^{M times L} , mathbf{B}=[mathbf{b}_1, cdots, mathbf{b}_L] in mathbb{R}^{N times L} ,即可用矩陣操作來表示生成 xi ,即 xi(mathcal{I}) = mathbf{A}mathbf{B}^T in mathbb{R}^{M times N}.
作者使用bilinear pooling對兩種特征提取器進行融合,再用於fine-grained分類,取得不錯的效果。bilinear pooling的形式簡單,便於梯度反向傳播,進而實現端到端的訓練。
- Second-order Pooling
Second-order Pooling最早出自ECCV2012的文章《Semantic segmentation with second-order pooling》,原文對Second-order Pooling的定義如下
由於Second-order Pooling用到瞭特征 x 的二階信息,所以在一些任務下能比一階信息表現更為優秀。
對比bilinear pooling的定義,不難發現,當 f_A=f_B 的時候,二者是等價的。也就是說,二階池化(Second-order Pooling)=同源雙線性池化(HBP,Homogeneous Bilinear Pooling)。
下面介紹bilinear pooling的各種改進。
- CBP: Compact Bilinear Pooling
CBP出自CVPR 2016《Compact bilinear pooling》一文,作者觀察到在分類問題中,提取的特征常常采用SVM或者logistic regression,而這兩種形式都可以被看作是線性核機器(linear kernel machines),具有如下的形式 <x(mathcal{I}_a), x(mathcal{I}_b)> 。
註意到
begin{align*} <x(mathcal{I}_a), x(mathcal{I}_b)> &= <text{vec}(xi(mathcal{I}_a)), text{vec}(xi(mathcal{I}_b))> \ &= <text{vec}(sum_i textbf{a}_itextbf{a}_i^T), text{vec}(sum_j textbf{b}_jtextbf{b}_j^T)> \ &= sum_isum_j <text{vec}(textbf{a}_itextbf{a}_i^T), text{vec}(textbf{b}_jtextbf{b}_j^T)> \ &= sum_isum_j <textbf{a}_i, textbf{b}_j>^2 end{align*}
如果我們能夠找到滿足 <phi(mathbf{a}), phi(mathbf{b})> approx <textbf{a}, textbf{b}>^2 的低維投影函數 phi(mathbf{a}) in mathbb{R}^d, d ll M times M ,那麼有
begin{align*} <x(mathcal{I}_a), x(mathcal{I}_b)> &= sum_isum_j <textbf{a}_i, textbf{b}_j>^2 \ &approx sum_i sum_j <phi(mathbf{a}_i), phi(mathbf{b}_j)> \ &=<sum_iphi(mathbf{a}_i), sum_jphi(mathbf{b}_j)> end{align*}
也就是說,當 <phi(mathbf{a}), phi(mathbf{b})> approx <textbf{a}, textbf{b}>^2 時,有 x(mathcal{I}_a) approx sum_iphi(mathbf{a}_i) 。基於這個思想,作者提出瞭采用瞭兩種方法 Random Maclaurin (RM)和Tensor Sketch (TS)對bilinear pooling進行降維。具體細節如下:
- MCBP: Multimodal Compact Bilinear Pooling
《Multimodal compact bilinear pooling for visual question answering and visual grounding》是EMNLP2016的文章。本文在CBP的基礎上提出瞭MCBP,並將其應用於看圖答題(VQA,visual question answering)領域。
註意到CBP是針對HBP進行改進的,對CBP的TS算法稍加改動,使其適用於融合不同模態的特征,即可得到MCBP,如下圖所示。
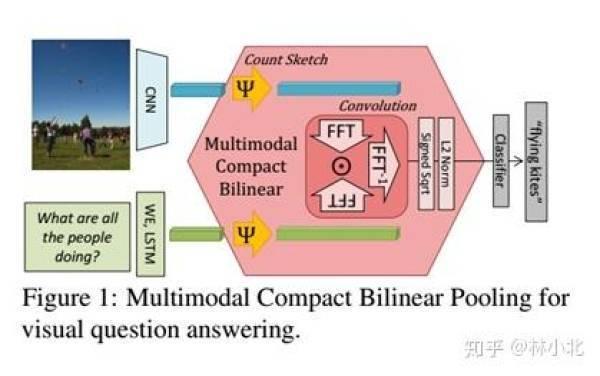
在得到MCBP模塊後,作者提出用於VQA的網絡結構如下:
這個結構相當容易理解,就是一共用到瞭兩次MCBP模塊,第一個MCBP融合瞭文本和圖像的特征進而用來提取圖像的attention,第二個MCBP則把圖像的attention特征與文本特征再一次融合,最終結果送入softmax分類器得到答案。
- LRBP:Low-rank Bilinear Pooling
LRBP出自CVPR2017的文章《Low-rank bilinear pooling for fine-grained classification》,與CBP一樣,都是假定采用的分類器是SVM來對HBP進行簡化。
考慮SVM問題
的最優解 bf{w}^* ,以及問題
的最優解 bf{W}^* ,作者證明瞭
並且bf{W}^* 是實對稱矩陣。實對稱矩陣的一大優點是可以進行特征值分解,即
如果用兩個低秩矩陣 bf{U}_+ 和 bf{U}_- 去近似bf{W}^*,則問題轉換為:
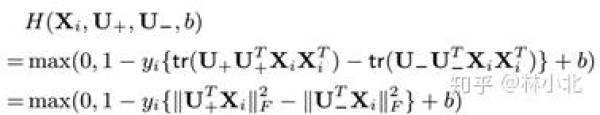
這樣就避免瞭原始bilinear pooling裡面 bf{X}bf{X}^T 的計算,降低瞭計算量。
- Grassmann Pooling
Grassmann Pooling出自ECCV 2018的文章《Grassmann Pooling as Compact Homogeneous Bilinear Pooling for Fine-Grained Visual Classification》,也是針對HBP的改進。
考慮形式為
的bilinear pooling,有引理如下:
也就是說,對矩陣 bf{A} 進行SVD分解,前k個左奇異向量組成的矩陣 bf{A}_k 是對矩陣 bf{A}的低秩最優逼近。
基於這個引理,作者提出瞭Grassmann pooling如下:
顯然,Grassmann pooling也能夠簡化bilinear pooling計算量。
上面提到的三種改進形式CBP、LRBP、Grassmann Pooling都是針對HBP的改進。MCBP直接對CBP改動用於多模態特征的融合,但是考慮到CBP的出發點是核函數,MCBP的改動其實有點站不住腳的。對於MBP的改進工作,主要是以MLB為基礎。MLB的核心是利用Hadamard積來簡化bilinear model的操作。在介紹MLB之前,先介紹一篇承上啟下的工作,把bilinear pooling和billinear model建立聯系。
- 從bilinear pooling到billinear model
《Factorized bilinear models for image recognition》是ICCV2017的文章,雖然本文也是針對HBP的研究,但成功地把bilinear model與bilinear pooling聯系起來。而後面的工作MLB正是從bilinear model的角度出發去改進MBP。
首先介紹bilinear model,對於特征向量 x 和特征向量 y ,bilinear model是指形如
的操作。
忽視bilinear pooling的歸一化操作,記HBP的特征為 text{vec}(sum_ibf{x_ix_i^T}) ,
在分類任務中,我們常常會把提取的特征送入全連接層再送入softmax層。作者發現,這個操作與bilinear model是等價的,即
其中 bf{W}_j 是全連接層的參數矩陣,而bf{W}_j^R是與其相對應的一個矩陣。既然bf{W}_j是需要通過學習得到的,那不如直接寫成bilinear model的形式,對bf{W}_j^R進行學習。也就是說,bilinear pooling與bilinear model是等價的。更令人欣喜的是,這個結論對於MBP也是適用的,所以後面MLB直接針對bilinear model進行改進。
基於這個發現,作者提出瞭Factorized bilinear model,把特征的一階信息和二階信息都利用起來,進而更好的fine-grained分類,其形式如下:
這裡利用低秩矩陣 bf{F} 來替代bf{W}_j^R,簡化瞭計算量。
- MLB:Multimodal Low-rank Bilinear Pooling
有瞭上篇工作的介紹,理解MLB就非常容易瞭,MLB出自ICLR2017的文章《 Hadamard product for low-rank bilinear pooling》。文章核心是用Hadamard積(就是按元素乘)來實現bilinear model,把
寫成瞭
這樣的好處是,利用低秩矩陣 bf{U_i} 及 bf{V_i} 來近似 bf{W}_i ,並且簡化瞭操作。
當希望bilinear model的輸出是向量的時候,隻需擴大矩陣 bf{U_i} 及 bf{V_i},並采用矩陣 bf{P} 控制輸出的長度即可,如下所示:
本文的寫作相當嚴謹,各個矩陣的尺寸大小均有註明,有興趣的讀者自行翻閱。
- MFB:Multi-modal factorized bilinear pooling
MFB出自ICCV2017《Multi-modal factorized bilinear pooling with co-attention learning for visual question answering》。本文的思路與MLB十分相似,不同點在於當希望bilinear model的輸出是向量的時候,本文直接把U和V變成瞭三維張量,再通過sum pooling來進行通道融合得到最後的輸出。
在MFB的基礎上,作者於《Beyond bilinear: Generalized multimodal factorized high-order pooling for visual question answering》一文中提出瞭MFH(Multi-modal factorized high-order pooling )。把MFB操作分為兩個階段Expand Stage和Squeeze Stage,MFH就是把MFB堆疊起來以得到高階信息,如下圖所示
作者成功地把MFB/MFH應用於VQA,提出的網絡結構如下:
這個結構與前文提到的《Multimodal compact bilinear pooling for visual question answering and visual grounding》相當類似,都是利用融合後的特征提取圖像的attention特征,再進而第二次融合進而用來分類。不同之處在於,作者模擬瞭人類“審題”的思維模式,先建立瞭文本的attention特征,再去考慮與圖像的特征融合。
前面介紹的工作,都是針對bilinear pooling的計算量過大而進行的改進。作為融合特征的有效方法,bilinear pooling在fine-grained分類和VQA都有不錯的發揮。這裡再簡要介紹bilinear pooling的幾篇應用。
- 應用於VQA領域的《Bilinear attention networks》
本文是MLB的續作,發表於NIPS2018。本文借助bilinear model的思想提出瞭bilinear attention的思想。常規的attention map是對單個特征的attention,output=feature * attention map,而本文提出的bilinear attention map則對兩個特征的attention, output=feature1 * bilinear attention map * feature2,表達式如下:
這個表達式與MLB十分相似,可以說是一脈相承。
本文提出的網絡結構如下所示,左圖通過MLB把圖像特征和文本特征融合,進而得到bilinear attention map,右圖則是把bilinear attention map用於進行圖像特征和文本特征的attention融合。該網絡較為復雜,有興趣的讀者自行翻閱原文。
- 應用於分類領域的《Hierarchical Bilinear Pooling for Fine-Grained Visual Recognition》
本文出自ECCV2018,核心思想是把不同層的特征通過bilinear pooling兩兩融合,最後concate後進行分類。
- 應用於ReID領域的《Part-Aligned Bilinear Representations for Person Re-Identification》
本文出自ECCV2018,核心是把行人的全局特征與局部特征(通過openpose預訓練得到)通過bilinear pooling融合,再進行檢索。
- 應用於三維物品識別領域的《Multi-View Harmonized Bilinear Network for 3D Object Recognition》
本文出自CVPR 2018,核心是利用HBP提取多視角特征。
- 應用於動作識別領域的《Deep Bilinear Learning for RGB-D Action Recognition》
本文出自ECCV 2018,基於bilinear model提出瞭bilinear block,來更好地融合多模態信息。