這裡是一則小廣告:
關註作者請點擊這裡哦:zdr0
我的專欄裡面不僅有學習筆記,也有一些科普文章,相信我的專欄不會讓您失望哦~大傢可以關註一下:數學及自然科學
記得點贊加收藏哦~
創作不易,請贊賞一下支持一下作者吧[期待]~
文章中如果有錯誤的話還請各位大佬多多斧正,感謝!
-盡力寫最好的講義,盡力寫最好的科普
推一下我的微信公眾號,掃碼即可關註哦!今後在知乎所發的文章都會同步到該公眾號當中(本文尚未同步,因為快考試瞭,所以很忙,抽時間會進行同步):
割集電壓法(復頻域)
boxed{bm{overset{otimes}{Y}}(s)cdotvec{overset{otimes}{U}}(s)=vec{overset{otimes}{J}}_0(s)}tag{1.1}
式 (1.1) 也可以寫為方程組的形式:
begin{pmatrix} overset{otimes}{Y}_{11}(s) & overset{otimes}{Y}_{12}(s) & ldots & overset{otimes}{Y}_{1n}(s) \ overset{otimes}{Y}_{21}(s) & overset{otimes}{Y}_{22}(s) & ldots & overset{otimes}{Y}_{2n}(s) \ vdots & vdots & ddots & vdots \ overset{otimes}{Y}_{n1}(s) & overset{otimes}{Y}_{n2}(s) & ldots & overset{otimes}{Y}_{nn}(s) end{pmatrix}cdot begin{pmatrix} overset{otimes}{U}_{1}(s) \ overset{otimes}{U}_{2}(s) \ vdots\ overset{otimes}{U}_{n}(s) end{pmatrix}=begin{pmatrix} overset{otimes}{J}_{1,0}(s) \ overset{otimes}{J}_{2,0}(s) \ vdots\ overset{otimes}{J}_{n,0}(s) end{pmatrix}.tag{1.2}
其中, bm{overset{otimes}{Y}}(s) 稱為標準化的割集導納矩陣, vec{overset{otimes}{U}}(s) 稱為割集電壓矢量, vec{overset{otimes}{J}}_0(s) 稱為標準化的電流源矢量。
下面我們來說一下割集電壓法的一般步驟 :
使用前提:所有的受控電流源的控制量必須為電壓 ;所有的支路必須為等效電流源支路,或者支路上隻能有理想電流源(包括受電壓控制的電流源)。
color{blue}{bm{rm{i).}}} 繪制電路圖的拓撲圖並且選擇樹枝和連枝,並確定基本割集 (隻包含一個樹枝的割集),如果發現需要電源搬移或者需要電源的等效變換或者兩者同時需要,請先跳至第 color{blue}{bm{rm{v}).}} 步,此外如果跳至第五步,那麼第 color{blue}{bm{rm{ii}).}},,color{blue}{bm{rm{iii}).}} 步就不必要做瞭(做瞭也沒影響);
color{blue}{bm{rm{ii}).}} 確定電路中總的支路個數 z ,總的節點個數 k 和總的子電路個數 s ;
color{blue}{bm{rm{iii}).}} 計算電路中的線性無關的節點方程的個數,即 p=k-s ,以決定 mathrm{dim}left( bm{overset{otimes}{Y}}(s)right) ;
color{blue}{bm{rm{iv}).}} 將樹枝電壓選作割集電壓 {overset{otimes}{U}}_i(s),quad i=1,2,ldots,n ,其方向與基本割集的方向一致,並將選擇好的割集電壓作為割集電壓矢量 vec{overset{otimes}{U}}(s) 中的元素,其餘所有的控制電壓均使用 vec{overset{otimes}{U}}(s) 中的元素進行表示;
color{blue}{bm{rm{v}).}} 全部支路都使用等效電流源支路(包括理想電流源或者受電壓控制的電流源)進行表示(如果可以的話,否則就需要進行電源搬移,之後再表示為等效電流源支路的形式,且如果出現的電源搬移則 mathrm{dim}left( bm{overset{otimes}{Y}}(s)right) 可能會改變,所以電源搬移後需要重新計算 mathrm{dim}left( bm{overset{otimes}{Y}}(s)right) );
color{blue}{bm{rm{vi}).}} 列寫非標準化的割集電壓方程組:
bm{overset{otimes}{Y}}_{OS}(s)cdotvec{overset{otimes}{U}}(s) =vec{overset{otimes}{J}}(s).tag{1.3}
其中, bm{overset{otimes}{Y}}_{OS}(s) 為非標準化的割集導納矩陣, vec{overset{otimes}{U}}(s) 為割集電壓矢量, vec{overset{otimes}{J}}(s) 為非標準化的電流源矢量。
第 rm{vi} 步的展開,即 bm{overset{otimes}{Y}}_{OS}(s) 和 vec{overset{otimes}{J}}(s) 的列寫方法:
- {overset{otimes}{Y}}_{ij,,OS}(s),quad(i=j): 屬於基本割集 i(j) 中的所有導納的和,符號全部為正;
- {overset{otimes}{Y}}_{ij,,OS}(s),quad(ine j): 同時屬於基本割集 i 與基本割集 j 的所有導納的和,當基本割集 i 中的樹枝與基本割集 j 中的樹枝方向相同(順)時為正,當基本割集 i 中的樹枝與基本割集 j 中的樹枝方向相反(逆)時為負;
- {overset{otimes}{J}}_{i}(s): 屬於基本割集 i 的所有電流源的和,當電流源的方向與基本割集 i 的方向相同時符號為負,當電流源的方向與基本割集 i 的方向相反時符號為正;
color{blue}{bm{rm{vii}).}} 將列好的式 (1.3) 標準化為式 (1.1) 。標準化的過程見算例。
割集電壓法算例(復頻域)
largebm{rm{Examplequad 1}:}
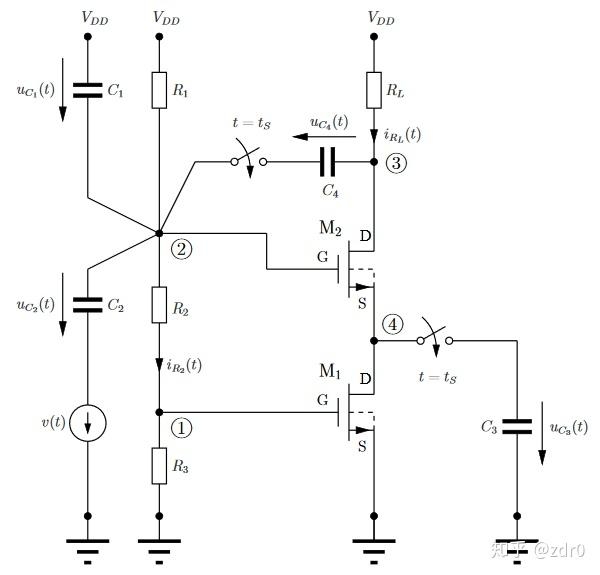 圖片1
圖片1
給定如上圖(圖片1)所示的大信號模型,其中包含兩個相同的 rm{NMOS-Transitor} M_1 和 M_2 ,四個線性時不變的電阻 R_i>0,,R_L>0,quad i=1,2,3 ,四個線性時不變的電容 C_i>0,quad i=1,2,3,4 ,此外還有一個理想的直流電壓源 V_{DD} 和一個理想的、非受控的小信號電壓源 v(t)=v_{KS}(t) 。其中兩個 rm{NMOS-Transitor} 的小信號模型均為圖片2所示:
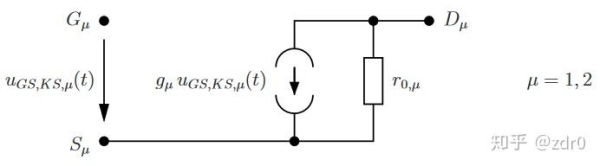
要求:請選擇樹枝,使得所選的樹枝包含 R_L,,R_2,,C_3,,C_4 。
請列寫圖片1中所示電路小信號模型的割集電壓方程。
largebm{rm{Solution}:}
在開始之前,我們首先要繪制出圖片1所示電路的小信號模型,如圖片3所示:
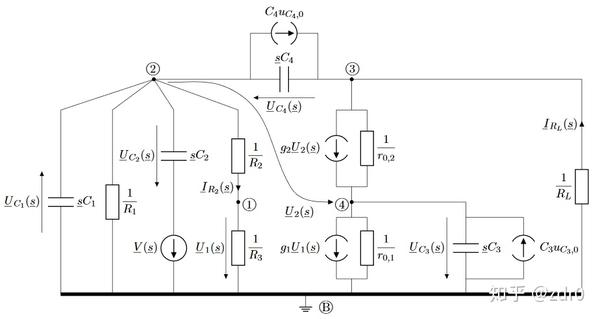 圖片3
圖片3
繪制小信號模型的之後要註意:
- 動態元件可能具有初值電源;
- 所有的控制量需要標註;
- 各個支路的電流或者電壓方向需要標註,以便用於可能的電源搬移,進而方便列寫變換方程。
下面,我們就按照步驟來詳細的體會一下回路電流法的過程:
color{blue}{bm{rm{i}).}} 首先由小信號模型判斷該電路不需要進行電源搬移和電源的等效變換。我們發現除瞭②號節點到地的四條支路中的一條以外,其餘的全部電路均以通過等效電流源支路進行瞭表示,所部不需要電源的搬移,但是需要先跳到第五步。而那條支路可以使用電源的等效變換,即:
圖片4
經過電源的等效變換之後,我們發現小信號模型中的所有支路都為等效電流源支路瞭,並且所有受控電流源的控制量均為電壓,所以本題滿足使用割集電壓法的條件。這樣小信號的拓撲圖如圖片5所示:
圖片5
其中實線為樹枝,虛線為連枝。註意,這裡的基本割集有四個 (FS_i:=i,quad i=1,2,3,4) ,且基本割集的方向需要通過屬於其的樹枝的方向進行確定;
color{blue}{bm{rm{ii}).}} 由於第 color{blue}{bm{rm{i}).}} 步中的拓撲圖是再進行完第 color{blue}{bm{rm{v}).}} 之後繪制的,所以,這一步可以省略。不過我們還是做一下。圖片2中所示電路的總的支路個數為 z=9 ,總的節點個數為 k=5 ,總的子電路的個數為 s=1 ;
color{blue}{bm{rm{iii}).}} 這一步也可以省略,但我們也做一下。電路中的線性無關的節點方程的個數為: p=k-s=5-1=4 ,所以 mathrm{dim}left( bm{overset{otimes}{Y}}(s)right)=4 (由於第 color{blue}{bm{rm{i}).}} 步中的拓撲圖是再進行完第color{blue}{bm{rm{v}).}} 之後繪制的,所以這個結果與第 color{blue}{bm{rm{v}).}} 步中的結果必然一致);
color{blue}{bm{rm{iv}).}} 圖片5中,樹枝為割集電壓,且割集電壓的方向要與割集的方向(樹枝電壓的方向)一致,且對比圖片3和圖片5可知控制電壓為:
U_1(s)=-{overset{otimes}{U}}_2(s)-{overset{otimes}{U}}_3(s)-{overset{otimes}{U}}_4(s),tag{1.4}
U_2(s)=-{overset{otimes}{U}}_1(s)-{overset{otimes}{U}}_2(s)-{overset{otimes}{U}}_3(s).tag{1.5}
color{blue}{bm{rm{v}).}} 見 color{blue}{bm{rm{i}).}}simcolor{blue}{bm{rm{iii}).}} ;
color{blue}{bm{rm{vi}).}} 按照步驟並根據電路的拓撲圖列寫非標準化的割集電壓方程組:
bm{overset{otimes}{Y}}_{OS}(s)cdotvec{overset{otimes}{U}}(s) =vec{overset{otimes}{J}}(s).tag{1.6}
bm{overset{otimes}{Y}}_{OS}(s)=begin{pmatrix} dfrac{1}{r_{0,1}}+dfrac{1}{r_{0,2}}+sC_3 & dfrac{1}{r_{0,2}} & 0 & 0\ dfrac{1}{r_{0,2}} & dfrac{1}{r_{0,2}}+dfrac{1}{R_L}+dfrac{1}{R_1}+dfrac{1}{R_3}+s(C_1+C_2) & dfrac{1}{R_1}+dfrac{1}{R_3}+s(C_1+C_2) &dfrac{1}{R_3} \ 0 & dfrac{1}{R_1}+dfrac{1}{R_3}+s(C_1+C_2) & dfrac{1}{R_1}+dfrac{1}{R_3}+s(C_1+C_2+C_4) &dfrac{1}{R_3} \ 0 & dfrac{1}{R_3} & dfrac{1}{R_3} & dfrac{1}{R_2}+dfrac{1}{R_3} end{pmatrix}.tag{1.7}
vec{overset{otimes}{J}}(s)=begin{pmatrix} g_2U_2(s)-g_1U_1(s)+C_3u_{C_3,0}\ g_2U_2(s)-sC_2V(s)\ -sC_2V(s)+C_4u_{C_4,0}\ 0 end{pmatrix}.tag{1.8}
color{blue}{bm{rm{vi}).}} 將式 (1.4),,(1.5) 代入到式 (1.8) 中:
vec{overset{otimes}{J}}(s)=begin{pmatrix} g_2left( -{overset{otimes}{U}}_1(s)-{overset{otimes}{U}}_2(s)-{overset{otimes}{U}}_3(s) right)-g_1left( -{overset{otimes}{U}}_2(s)-{overset{otimes}{U}}_3(s)-{overset{otimes}{U}}_4(s) right)+C_3u_{C_3,0}\ g_2left( -{overset{otimes}{U}}_1(s)-{overset{otimes}{U}}_2(s)-{overset{otimes}{U}}_3(s) right)-sC_2V(s)\ -sC_2V(s)+C_4u_{C_4,0}\ 0 end{pmatrix}.tag{1.9}
並標準化式 (1.7) 和式 (1.9) :
bm{overset{otimes}{Y}}(s)=begin{pmatrix} dfrac{1}{r_{0,1}}+dfrac{1}{r_{0,2}}+sC_3+color{red}{g_2} & dfrac{1}{r_{0,2}}+color{red}{g_2}-color{red}{g_1} & 0+color{red}{g_2}-color{red}{g_1} & 0-color{red}{g_1}\ dfrac{1}{r_{0,2}}+color{red}{g_2} & dfrac{1}{r_{0,2}}+dfrac{1}{R_L}+dfrac{1}{R_1}+dfrac{1}{R_3}+s(C_1+C_2)+color{red}{g_2} & dfrac{1}{R_1}+dfrac{1}{R_3}+s(C_1+C_2)+color{red}{g_2} &dfrac{1}{R_3} \ 0 & dfrac{1}{R_1}+dfrac{1}{R_3}+s(C_1+C_2) & dfrac{1}{R_1}+dfrac{1}{R_3}+s(C_1+C_2+C_4) &dfrac{1}{R_3} \ 0 & dfrac{1}{R_3} & dfrac{1}{R_3} & dfrac{1}{R_2}+dfrac{1}{R_3} end{pmatrix}.tag{1.10}
vec{overset{otimes}{J}}_0(s)=begin{pmatrix} C_3u_{C_3,0}\ -sC_2V(s)\ -sC_2V(s)+C_4u_{C_4,0}\ 0 end{pmatrix}.tag{1.11}
最後得:
bm{overset{otimes}{Y}}(s)cdotvec{overset{otimes}{U}}(s) =vec{overset{otimes}{J}}_{0}(s).tag{1.12}
式 (1.12) 即為所求。