一、前言
論文鏈接:
代碼鏈接:
效果比較:不加任何數據增強、多尺度訓練和測試等tricks下,將RetinaNet-Res50上的Smooth L1 Loss換成KLD,模型在DOTA1.0數據集上的 AP_{50} 從65.73%提高到71.28%, AP_{75} 從32.31%提升到44.48%。
已經看過GWD的朋友可能會有這樣子的想法:“這篇論文不就是把Wasserstein Distance換成瞭Kullback-Leibler Divergence瞭嗎?”。說的其實沒錯,但是有點片面瞭,這篇文章主要貢獻是從理論上分析為什麼Kullback-Leibler Divergence會比Wasserstein Distance要好。具體來說,GWD的側重點在於分析將框的表示從 (x,y,w,h,theta) 轉換成二維高斯分佈 (mu,Sigma) 的好處,也就是解決瞭邊界問題、類正方形檢測問題、損失和評估不一致問題。而這篇文章從在這個基礎上繼續探究轉換參數之後使用什麼樣分佈距離度量方式比較好,主要從高精度檢測和尺度不變性來解釋,並給出瞭理論上的證明。
二、歸納式的旋轉回歸損失設計
對於常見的通用檢測模型(水平框檢測),模型通常是通過回歸四個偏移量的形式來進行框位置和大小的預測:
t_{x}^{p}=frac{x_{p}-x_{a}}{w_{a}}, t_{y}^{p}=frac{y_{p}-y_{a}}{h_{a}}, t_{w}^{p}=lnleft(frac{w_{p}}{w_{a}}right), t_{h}^{p}=lnleft(frac{h_{p}}{h_{a}}right)
來匹配實際的偏移量:
t_{x}^{t}=frac{x_{t}-x_{a}}{w_{a}}, t_{y}^{t}=frac{y_{t}-y_{a}}{h_{a}}, t_{w}^{t}=lnleft(frac{w_{t}}{w_{a}}right), t_{h}^{t}=lnleft(frac{h_{t}}{h_{a}}right)
借鑒於此,目前絕大多數的旋轉目標檢測在上面的基礎上加上瞭角度參數的回歸:
t_{theta}^{p}=f(theta_{p}-theta_{a}), t_{theta}^{t}=f(theta_{t}-theta_{a})
其中 f(cdot) 用於處理角度周期性的函數,比如三角函數、取餘函數等。
然後回歸損失也常采用 L_{n}-norm:
L_{reg} = l_{n}text{-norm}left(Delta t_{x}, Delta t_{y}, Delta t_{w}, Delta t_{h}, Delta t_{theta}right)
其中 Delta t_{x} = t_{x}^{p} – t_{x}^{t} = frac{Delta x}{w_{a}},Delta t_{y} = t_{y}^{p} – t_{y}^{t} = frac{Delta y}{h_{a}},Delta t_{w} = t_{w}^{p} – t_{w}^{t} = ln(frac{w_{p}}{w_{t}} ), Delta t_{h} = t_{h}^{p} – t_{h}^{t} = ln(frac{h_{p}}{h_{t}}), Delta t_{theta} = t_{theta}^{p} – t_{theta}^{t} = Delta theta。
很明顯這種擴展方式屬於歸納法。五個參數獨立優化使得我們需要根據不同的數據集特點進行權重的調整,比如大長寬比目標可能需要著重關註角度參數,小目標則需要關註中心點參數,因為這些參數的輕微偏移都會造成這些目標預測精準度(IoU)的急劇下降。
三、演繹式的旋轉回歸損失設計
3.1 GWD的回顧
為瞭打破歸納式(induction)的設計范式,我們計劃采用演繹(deduction)設計范式,兩者的比較如下圖所示:
水平框作為旋轉框的一種特殊情況,我認為從水平檢測的回歸損失擴展出旋轉回歸損失是不準確的(圖a)。盡管我們常說水平檢測為“通用檢測”,但從算法設計上來看旋轉檢測顯得更加“通用”。因此我們采用瞭圖b的設計思路,先單獨設計旋轉回歸損失(這個損失無法簡單從水平回歸損失擴展出來),然後這個損失在水平情況下可以推導出水平回歸損失。
和GWD的做法一致,我們先把旋轉矩形(x,y,w,h,theta) 轉換成一個二維的高斯分佈(mu,Sigma):
轉換關系如下:
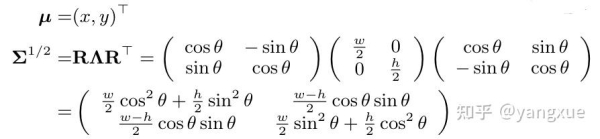
GWD的這種做法解決瞭邊界問題、類正方形檢測問題、損失和評估不一致問題。但是這篇文章的重點不是這,而是找到比Wasserstein Distance更適合旋轉檢測的分佈度量。先回顧一下Wasserstein Distance的公式:
mathbf{D}_{w}(mathcal{N}_{p}, mathcal{N}_{t})^{2}=underbrace{leftlVert bm{mu}_{p}-bm{mu}_{t}rightrVert_{2}^{2}}_{text{center distance}}+underbrace{mathbf{Tr}(bm{Sigma}_{p}+bm{Sigma}_{t}-2(bm{Sigma}_{p}^{1/2}bm{Sigma}_{t}bm{Sigma}_{p}^{1/2})^{1/2})}_{text{coupling terms about $h_{p}$, $w_{p}$ and } theta_{p}}
由這個公式可以看到,Wasserstein Distance可以分為兩項,一項是兩個分佈(旋轉矩形)中心點的歐式距離,另一項是關於 h,w,theta 三項的耦合項。盡管這個耦合項的引入有利於高精度檢測,但是第一項的單獨優化會使得檢測結果中心點出現偏移(具體原因我們會在後面分析)。另外,第一項還使得GWD不具備尺度不變性,從這看當初使用GWD來近似IoU loss有點名不副實瞭。
再來看一下在水平情況下,即 theta=0^circ ,上式就可以化簡成如下公式: mathbf{D}_{w}^{h}(mathcal{N}_{p}, mathcal{N}_{t})^{2}=lVert bm{mu}_{p}-bm{mu}_{t}rVert_{2}^{2}+lVert bm{Sigma}_{p}^{1/2}-bm{Sigma}_{t}^{1/2} rVert_{F}^{2}/ qquad qquad qquad qquad qquad quad =(x_{p}-x_{t})^2+(y_{p}-y_{t})^2+left((w_{p}-w_{t})^2+(h_{p}-h_{t})^2right)/4/ quad =l_{2}text{-norm}(Delta x, Delta y, Delta w/2, Delta h/2)
這和水平框檢測使用的回歸損失就很像瞭,隻不過一個是通過偏移量來計算損失, 一個是通過絕對坐標來計算損失瞭。從這看出,GWD也算是屬於演繹法的一種,隻不過這個損失函數並不完美。
總結一下GWD的缺點:1)中心點單獨優化會出現檢測結果的位置偏移。2)不具備尺度不變性。3)水平情況下退化出來的回歸損失和常用的回歸損失還是存在不一致(這個不重要)。
3.2 Kullback-Leibler Divergence
接下來就正式介紹文章的重頭戲瞭,Kullback-Leibler Divergence (KLD)為何能彌補上面的三個缺點。首先我們來看一下KLD的具體表達式,由於KLD具有不對稱性,它有兩種形式,分別如下:
mathbf{D}_{kl}(mathcal{N}_{p}||mathcal{N}_{t})=underbrace{frac{1}{2}(bm{mu}_{p}-bm{mu}_{t})^{top}bm{Sigma}_{t}^{-1}(bm{mu}_{p}-bm{mu}_{t})}_{text{term about $x_{p}$ and $y_{p}$}}+underbrace{frac{1}{2}mathbf{Tr}(bm{Sigma}_{t}^{-1}bm{Sigma}_{p}) + frac{1}{2}ln frac{|bm{Sigma}_{t}|}{|bm{Sigma}_{p}|}}_{text{coupling terms about $h_{p}$, $w_{p}$ and } theta_{p}}-1
或者
mathbf{D}_{kl}(mathcal{N}_{t}||mathcal{N}_{p})=underbrace{frac{1}{2}(bm{mu}_{p}-bm{mu}_{t})^{top}bm{Sigma}_{p}^{-1}(bm{mu}_{p}-bm{mu}_{t})+frac{1}{2}mathbf{Tr}(bm{Sigma}_{p}^{-1}bm{Sigma}_{t}) + frac{1}{2}ln frac{|bm{Sigma}_{p}|}{|bm{Sigma}_{t}|}}_{text{chain coupling of all parameters}}-1
mathbf{D}_{kl}(mathcal{N}_{p}||mathcal{N}_{t}) 和GWD一樣也是參數半耦合的,但是它的第一項中引入瞭 bm{Sigma}_{t}^{-1} ,這個對於中心點的優化起瞭非常大的作用。在 mathbf{D}_{kl}(mathcal{N}_{t}||mathcal{N}_{p}) 中,部分不同參數耦合優化,形成瞭一種鏈式耦合的關系。盡管兩者區別挺大,但我們發現它們優化的機制是差不多的,這裡就以簡單的mathbf{D}_{kl}(mathcal{N}_{p}||mathcal{N}_{t}) 來作為示例。首先我們將式子中的三項列出來: left (bm{mu}_{p}-bm{mu}_{t}right)^{top}bm{Sigma}_{t}^{-1}(bm{mu}_{p}-bm{mu}_{t})=frac{4left(Delta xcostheta_{t}+Delta ysintheta_{t}right)^{2}}{w_{t}^{2}} + frac{4left(Delta ycostheta_{t}-Delta xsintheta_{t}right)^{2}}{h_{t}^{2}}
mathbf{Tr}(bm{Sigma}_{t}^{-1}bm{Sigma}_{p})= frac{h_{p}^{2}}{w_{t}^{2}}sin^{2}Delta theta+frac{w_{p}^{2}}{h_{t}^{2}}sin^{2}Delta theta+frac{h_{p}^{2}}{h_{t}^{2}}cos^{2}Delta theta+frac{w_{p}^{2}}{w_{t}^{2}}cos^{2}Delta theta
ln frac{|bm{Sigma}_{t}|}{|bm{Sigma}_{p}|}=ln frac{h_{t}^{2}}{h_{p}^{2}} + ln frac{w_{t}^{2}}{w_{p}^{2}}
其中 Delta x=x_{p}-x_{t}, Delta y=y_{p}-y_{t}, Delta theta=theta_{p}-theta_{t} 。
3.3 高精度檢測分析
我們通過梯度(公式一時爽,求導火葬場)來進行分析,為何KLD為何適合於高精度的旋轉檢測。不失一般性,我們令 theta_{t}=0^{circ} ,則有
frac{partial f_{kl}(mu_{p})}{partialmu_{p}}= left(frac{4}{w_{t}^{2}}Delta x, frac{4}{h_{t}^{2}}Delta yright)^{top}
權重 1/w_{t}^{2} 和 1/h_{t}^{2} 使得模型可以根據目標的尺度來動態調整權重。比如,當目標非常小或者某一條邊比較短的時候,模型會增大相應方向的梯度,以慎重進行位置的偏移的優化。因為對於這類目標來說,很小的位置偏移都會造成IoU的急劇下降。當 theta_{t} neq 0^{circ} 時,目標的偏移量( Delta x 和 Delta y )的梯度會根據角度進行動態調整以提供更好的優化。相比之下,GWD和 L_{2} 關於偏移量的梯度分別是 frac{partial f_{w}(mu_{p})}{partialmu_{p}}=(2Delta x, 2Delta y)^{top} 和 frac{partial f_{L_{2}}(mu_{p})}{partialmu_{p}}=(frac{2}{w_{a}^{2}}Delta x, frac{2}{h_{a}^{2}}Delta y)^{top} 。前者既和角度參數無關,也不會根據目標的尺度來進行動態調整。後者盡管也有權重 1/w_{a}^{2} 和 1/h_{a}^{2},但這是anchor的兩邊,對於使用水平anchor來說的絕大多數旋轉檢測器來說,這個是不夠準確的,因為水平anchor的長寬無法反映實際目標的尺寸(尤其在目標有一定傾斜角的時候)。先看一下三種方法的可視化對比:
Visual comparison between Smooth L1 loss (left), GWD (middle) and KLD (right)
可以看到Smooth L1 loss和GWD的中心點都有輕微的偏移,而KLD就十分準確,這是KLD能實現高精度旋轉檢測的其中一點。
分析到這裡,讓我對使用旋轉還是水平anchor有瞭一些新的理解,這些內容文章中沒有寫。回顧我之前的工作R^3Det,我在選baseline的時候做過使用水平anchor和旋轉anchor的實驗。水平anchor可以提供較高的recall(水平anchor與gt的水平外接矩形的IoU作為樣本采樣的依據),而且需要設置的anchor比較少,但是anchor質量不佳(anchor與gt的IoU不高);而旋轉anchor盡管能提供較高質量的樣本,但是需要設置的anchor數量巨大且能匹配到的正樣本數量少,即recall低。這兩種方法的可視化情況是,水平anchor的方法在密集場景預測目標的中心點偏移嚴重,而旋轉anchor則預測的比較準,下圖所示:
一開始我以為是因為水平anchor的樣本質量太差,會引入過多幹擾信息,但現在一想,在image-level(全卷積形式,另一種是二階段那種全鏈接形式的instance-level)的預測方式下,中心點的優化好像和anchor是什麼形式沒啥關系(全鏈接的形式可能就有關系瞭,因為會把一塊區域裁剪下來,這塊區域包含很多背景噪聲區域,影響進一步的回歸預測),因為不管是水平還是旋轉anchor,它們中心點是同個地方。旋轉還是水平的anchor對 w,h,theta 參數的影響會比較大。
現在總算明白瞭,偏移的現象和中心點參數梯度的權重有關,旋轉anchor能提供高質量的先驗,它的長寬和gt接近( w_{a}=w_{t}, h_{a}=h_{t} ),所以基於旋轉anchor的方法中心點偏移不嚴重,而水平anchor的長寬沒法反應實際gt的尺寸大小,因此偏移嚴重。一種解決辦法是像R^3Det一樣,加一個精修階段,在精修階段中水平anchor已經被回歸成靠近gt的旋轉框瞭,那麼精修階段的候選框相當於旋轉anchor一樣,最後中心點偏移也就不嚴重瞭。
言歸正傳,對兩邊 h_{p} 和 w_{p}求梯度,我們有: frac{partial f_{kl}(bm{Sigma}_{p})}{partial ln{h_{p}}}= frac{h_{p}^{2}}{h_{t}^{2}}cos^{2}Delta theta + frac{h_{p}^{2}}{w_{t}^{2}}sin^{2}Delta theta – 1, quad frac{partial f_{kl}(bm{Sigma}_{p})}{partial ln{w_{p}}}= frac{w_{p}^{2}}{w_{t}^{2}}cos^{2}Delta theta + frac{w_{p}^{2}}{h_{t}^{2}}sin^{2}Delta theta – 1
我們可以看到, 兩邊 h_{p} 和 w_{p}的梯度和角度差 Delta theta 有關。當 Delta theta=0^{circ} 時, frac{partial f_{kl}(bm{Sigma}_{p})}{partial ln{h_{p}}}= frac{h_{p}^{2}}{h_{t}^{2}} – 1, frac{partial f_{kl}(bm{Sigma}_{p})}{partial ln{w_{p}}}= frac{w_{p}^{2}}{w_{t}^{2}} -1 ,這意味著較小的目標尺度會導致其匹配到更大的損失。 這是符合認知的,因為較小的邊需要更高的匹配精度。再來看角度參數的梯度:
frac{partial f_{kl}(bm{Sigma}_{p})}{partialtheta_{p}}= left(frac{h_{p}^{2}-w_{p}^{2}}{w_{t}^2}+frac{w_{p}^{2}-h_{p}^{2}}{h_{t}^{2}}right)sin{2Delta theta}
角度差Delta theta的優化又受到h_{p} 和 w_{p}的的影響。當 w_{p}=w_{t}, h_{p}=h_{t} 時,我們有 frac{partial f_{kl}(bm{Sigma}_{p})}{partialtheta_{p}}= left(frac{h_{t}^{2}}{w_{t}^2}+frac{w_{t}^{2}}{h_{t}^{2}} – 2right)sin{2Delta theta} geq sin{2Delta theta} ,當目標是正方形( w_{t}=h_{t} )的時候取到等號。而當目標長寬比慢慢變大的時候,整個式子的值就會變大,也就是意味著對角度優化更加看重。這個優化機制是非常好的,我們知道對於長寬比越大的目標來說,它受角度差的影響就越大,IoU會產生急劇下降。這是KLD能實現高精度旋轉檢測的另一個重要原因,從上上圖來看,KLD角度的預測更加精準。我們來看一下三種損失函數對於每個參數梯度的直觀比較:
1)對於參數 Delta x 和 Delta y ,KLD在短邊方向上的梯度值變化非常明顯,而GWD和 L_{2} 並不受邊的長短的影像;
2)對於 Delta h 和 Delta w,KLD也具有上條差不多的性質,且這種變化對於長寬比越大的目標表現的越明顯;
3)對於 Delta theta ,KLD會根據長寬比的增大而動態增大梯度。相比之下,GWD也有相近的性質,但是變化更弱,而L_{2}對Delta theta的優化不受長寬比的影響。
mathbf{D}_{kl}(mathcal{N}_{t}||mathcal{N}_{p})雖然求導更加復雜,但是結論是基本一致的,求導過程可以看文章的附錄部分。總結來說,參數在KLD損失中的學習過程是根據目標的形狀進行自我調節的,有許多動態優化策略。
3.4 尺度不變性的證明
很明顯,GWD和 L_{2}不具有尺度不變性,那麼我們接下來證明KLD具有這一性質。對於兩個已知的高斯分佈 mathbf{X}_{p} sim mathcal{N}_{p}(bm{mu}_{p},bm{Sigma}_{p}) 和 mathbf{X}_{t} sim mathcal{N}_{t}(bm{mu}_{t},bm{Sigma}_{t}) ,假設有一個滿秩的矩陣 mathbf{M} ( |mathbf{M}|neq 0 ),我們有 :
mathbf{X}_{p^{'}} =mathbf{M}mathbf{X}_{p} sim mathcal{N}_{p}(mathbf{M}bm{mu}_{p},mathbf{M}bm{Sigma}_{p}mathbf{M}^{top}), mathbf{X}_{t^{'}}=mathbf{M}mathbf{X}_{t} sim mathcal{N}_{t}(mathbf{M}bm{mu}_{t},mathbf{M}bm{Sigma}_{t}mathbf{M}^{top}),
我們將其分別標記為 mathcal{N}_{p^{'}} 和 mathcal{N}_{t^{'}} ,那麼它們的KLD計算如下: mathbf{D}_{kl}(mathcal{N}_{p^{'}}||mathcal{N}_{t^{'}})=frac{1}{2}(bm{mu}_{p}-bm{mu}_{t})^{top}mathbf{M}^{top}(mathbf{M}^{top})^{-1}bm{Sigma}_{t}^{-1}mathbf{M}^{-1}mathbf{M}(bm{mu}_{p}-bm{mu}_{t})/ qquad qquad qquad qquad +frac{1}{2}mathbf{Tr}left((mathbf{M}^{top})^{-1}bm{Sigma}_{t}^{-1}mathbf{M}^{-1}mathbf{M}bm{Sigma}_{p}mathbf{M}^{top}right)+frac{1}{2}ln frac{|mathbf{M}||bm{Sigma}_{t}||mathbf{M}^{top}|}{|mathbf{M}||bm{Sigma}_{p}||mathbf{M}^{top}|}-1/ qquad qquad qquad qquad =frac{1}{2}(bm{mu}_{p}-bm{mu}_{t})^{top}bm{Sigma}_{t}^{-1}(bm{mu}_{p}-bm{mu}_{t})+frac{1}{2}mathbf{Tr}left(mathbf{M}^{top}(mathbf{M}^{top})^{-1}bm{Sigma}_{t}^{-1}mathbf{M}^{-1}mathbf{M}bm{Sigma}_{p}right)+frac{1}{2}ln frac{|bm{Sigma}_{t}|}{|bm{Sigma}_{p}|}-1/ =mathbf{D}_{kl}(mathcal{N}_{p}||mathcal{N}_{t})
因此KLD其實是具有仿射不變性的,包括瞭尺度不變性。當 mathbf{M}=kmathbf{I} ( mathbf{I} 表示單位矩陣)時,KLD的尺度不變性就被證明瞭。相比於GWD和 L_{2},KLD更能近似不可導的旋轉IoU損失來解決損失與評估不一致的問題。下圖比較瞭三個損失函數關於在不同尺度下的曲線變化:
3.5 KLD在水平情況下的退化公式
在水平特殊情況下,KLD退化成如下表達式: mathbf{D}_{kl}^{h}(mathcal{N}_{p}||mathcal{N}_{t})=frac{1}{2}left(frac{w_{p}^2}{w_{t}^2}+frac{h_{p}^{2}}{h_{t}^{2}}+frac{4Delta^{2}x}{w_{t}^{2}}+frac{4Delta^{2}y}{h_{t}^{2}}+ln frac{w_{t}^{2}}{w_{p}^{2}}+ln frac{h_{t}^{2}}{h_{p}^{2}}-2right)/ qquad qquad qquad =2l_{2}text{-norm}(Delta t_{x}, Delta t_{y})+l_{1}text{-norm}(Delta t_{w}, Delta t_{h})+frac{1}{2}l_{2}text{-norm}(frac{1}{Delta t_{w}}, frac{1}{Delta t_{h}}) -1
前兩項就和常見的水平回歸損失非常像瞭。
3.6 KLD的變體
我們在論文中對KLD的多種變體進行瞭研究,主要包括JS散度等,主要是為瞭探究KLD的不對稱性對結果的影響大不大。
mathbf{D}_{kl_min(max)}(mathcal{N}_{p}||mathcal{N}_{t})=min(max)left(mathbf{D}_{kl}(mathcal{N}_{p}||mathcal{N}_{t}), mathbf{D}_{kl}(mathcal{N}_{t}||mathcal{N}_{p})right)/ mathbf{D}_{js}(mathcal{N}_{p}||mathcal{N}_{t})=frac{1}{2}left(mathbf{D}_{kl}left(mathcal{N}_{t}||frac{mathcal{N}_{p}+mathcal{N}_{t}}{2}right)+mathbf{D}_{kl}left(mathcal{N}_{p}||frac{mathcal{N}_{p}+mathcal{N}_{t}}{2}right)right)/ mathbf{D}_{jef}(mathcal{N}_{p}||mathcal{N}_{t})=mathbf{D}_{kl}(mathcal{N}_{t}||mathcal{N}_{p})+mathbf{D}_{kl}(mathcal{N}_{p}||mathcal{N}_{t})
四、實驗分析
文章一共使用瞭7個數據集,在不同檢測器上進行瞭非常充足的實驗。
首先我們對KLD不同變體在兩個數據集上進行瞭實驗,發現最後的效果是差不多的,排除瞭不對稱性對結果的幹擾。

然後我們在3種數據集和2種檢測器上進行瞭高精度檢測實驗,我們發現KLD幾乎吊打另外兩種損失函數。
隨後我們在一些更具有挑戰性的數據集上進行瞭驗證實驗,包括DOTA-v1.5和DOTA-v2.0(包含很多像素值小於10的目標),KLD依舊表現出色。

我們還在相同環境下做瞭不同方法(均在我開源的benchmark上支持)的對比實驗,KLD幾乎也是在各方面勝出。
在水平檢測任務上(COCO數據集),KLD也是和GIoU等常見損失函數保持差不多的水平。
最後在DOTA-v1.0的SOTA實驗中,我們也取得瞭當前所發表論文裡的最高性能。
五、小結
盡管KLD看起來很完美,但是也存在一些問題,比如兩個相同大小相同位置的正方形目標,其中一個正方形不管怎麼旋轉,KLD的值始終是0,因為此時高斯分佈是一個圓形的,而實際的IoU是在變化的。還有一個問題是,KLD依舊局限於旋轉矩形的檢測,無法直接擴展在四邊形或者多邊形的檢測。有問題是好事,大傢可以接著改進接著發paper嘛~.~
如果大佬們有什麼改進想法或者相關的idea,歡迎找我交流,微信或者知乎都可。我的主頁有我的微信,當然非誠勿擾。